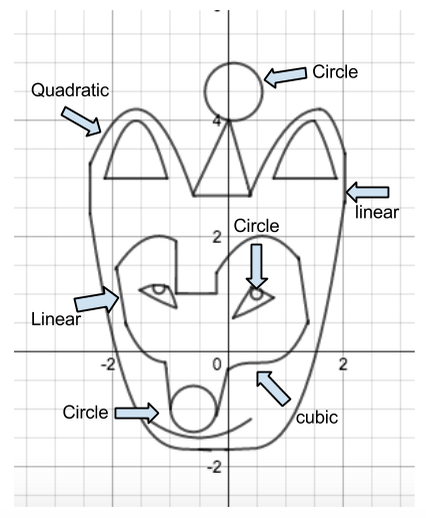
POW 5
Unit 4 - Desmos Drawing and Function Families
Unit 3 Reflection.
In unit 3 the most interesting content I have learned is how to use volume, space and surface area. These have helped me grow mathematically by making me go further into different equations and learning how to use a calculator correctly. Unit 2 has also made me think and visualize in 3D solids. For example, POW 4. Lastly, forming equations has taught me how important it is to have different equations for varying objects so you can have different outcomes.
POW 4
POW: What is the optimal combination of azimuth and tilt to maximize solar gain (kWh per year) from a 5kW photovoltaic system
Pow 1 Slices of Pie
Problem Statement:
For a given amount of cuts, can we determine the maximum amount of pieces we can get in the pie?
Process:
I started by first making circles on graph paper the I dove right in not thinking of what to do. I was astonished that I did my first five cut with one try. I knew the maximum because in the scale I was given, I saw a pattern of the number of cuts plus the number of pieces maximum = the maximum number of cuts for the next row. The next thing I did was try to do the other cuts from 6-10 doing this it was a struggle because not knowing how to solve it. After a while the teacher told me that all lines have to cross the one before and the one before that. After hearing this problem solving became easier to me but I still had to figure out how the equation. Then I noticed a pattern by looking at the table; that pattern is the maximum number of pieces increasing chronologically. For example from one to two the difference is a single unit. From two to four there is a two piece difference, from four to seven a three piece difference.
X = # of cuts Y = # of maximum pieces
0 1
1 2
2 4
3 7
4 11
5 16
6 22
7 29
8 37
9 46
10 56
Solution:
In the end the whole class sat down and went over different equations. The one that I chose was the second one we went over which follows:
Equation: f(5)=f(4)+5=11+5=16
Extension: I decided instead of doing circular pies, I wanted to do a square pie and how many cuts that would take to get the maximum number of pieces.
Self-Evaluation:
What I will take away from this is not to rush into a problem and to take your time and think it through. Also, I will remember all the equations we were taught.
For a given amount of cuts, can we determine the maximum amount of pieces we can get in the pie?
Process:
I started by first making circles on graph paper the I dove right in not thinking of what to do. I was astonished that I did my first five cut with one try. I knew the maximum because in the scale I was given, I saw a pattern of the number of cuts plus the number of pieces maximum = the maximum number of cuts for the next row. The next thing I did was try to do the other cuts from 6-10 doing this it was a struggle because not knowing how to solve it. After a while the teacher told me that all lines have to cross the one before and the one before that. After hearing this problem solving became easier to me but I still had to figure out how the equation. Then I noticed a pattern by looking at the table; that pattern is the maximum number of pieces increasing chronologically. For example from one to two the difference is a single unit. From two to four there is a two piece difference, from four to seven a three piece difference.
X = # of cuts Y = # of maximum pieces
0 1
1 2
2 4
3 7
4 11
5 16
6 22
7 29
8 37
9 46
10 56
Solution:
In the end the whole class sat down and went over different equations. The one that I chose was the second one we went over which follows:
Equation: f(5)=f(4)+5=11+5=16
Extension: I decided instead of doing circular pies, I wanted to do a square pie and how many cuts that would take to get the maximum number of pieces.
Self-Evaluation:
What I will take away from this is not to rush into a problem and to take your time and think it through. Also, I will remember all the equations we were taught.
Semester 1
POW: Boredom knight no longer
For the chess board puzzle we were given a sheet of paper that had a puzzle of switching black knights with white knights in a 3 x 3 square. It was very hard to switch them but I found out it was possible. It took me five attempts to figure out the puzzle. The first two attempts were unsuccessful. The third try I was able to figure it out within 20 moves. The fourth try I got it within 14 moves. I finally figured out an algorithm where I had to rotate the pieces individually. I focused on this approach my fifth try and got it within ten moves. An interesting thing I noticed at the end was that I can figure this puzzle in one move. All I needed to do was rotate the puzzle 180 degrees. This was a very stimulating puzzle.
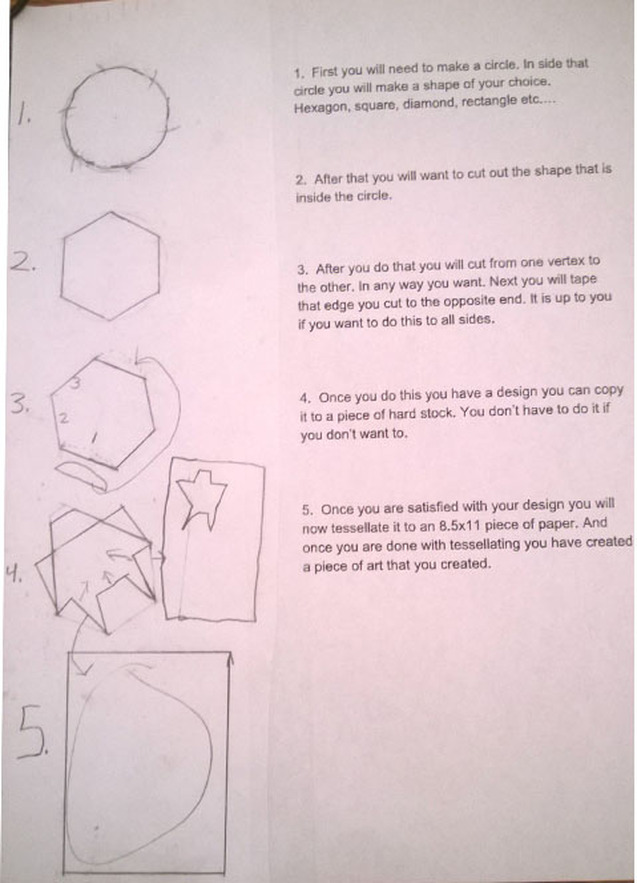
Tessellation project
1. What is the idea/theme behind your tessellation?
My theme was going to be a dog but I soon found out that it did not tessellate so I found a new design and I saw in it that it was a fish. Now my idea is fish. It started out as a hexagon then as I cut. It took shape into a fish then the next step was to put it on an 8x11 as soon as I did that I was told to put it on another 8x11 I put them together and made a good tessellating project.
2. What polygon did you start with and how did you alter it.
I started out with a hexagon the way the shape translated across the page was over 1 then down 2.
4. Are tessellations math or art? Back up your answer.
In my opinion it is both because every curve has a mathematical idea. But on the other hand art is a creation that is created by color.
My theme was going to be a dog but I soon found out that it did not tessellate so I found a new design and I saw in it that it was a fish. Now my idea is fish. It started out as a hexagon then as I cut. It took shape into a fish then the next step was to put it on an 8x11 as soon as I did that I was told to put it on another 8x11 I put them together and made a good tessellating project.
2. What polygon did you start with and how did you alter it.
I started out with a hexagon the way the shape translated across the page was over 1 then down 2.
4. Are tessellations math or art? Back up your answer.
In my opinion it is both because every curve has a mathematical idea. But on the other hand art is a creation that is created by color.